Rumus Jumlah dan Selisih Dua Sudut Perbandingan Trigonometri

Materi Matematika SMA

Pada postingan kali ini kami akan membahas tentang materi Rumus Jumlah dan Selisih Dua Sudut Perbandingan Trigonometri. Materi ini merupakan materi Matematika Peminatan Kelas XI pada kurikulum 2013. Silahkan disimak!

Rumus jumlah dan selisih dua sudut pada trigonometri adalah:

• @$ \sin \left ( A+B \right )=\sin A \cdot \cos B+\sin B \cdot \cos A @$
• @$ \sin \left ( A-B \right )=\sin A \cdot \cos B-\sin B \cdot \cos A @$
• @$ \cos \left ( A+B \right )=\cos A \cdot \cos B-\sin A \cdot \sin B @$
• @$ \cos\left ( A-B \right )=\cos A \cdot \cos B + \sin A \cdot \sin A @$
• @$ \tan \left ( A+B \right )=\dfrac{ \tan A+ \tan B}{1- \tan A\cdot \tan B} @$
• @$ \tan \left ( A-B \right )= \dfrac{ \tan A - \tan B}{1+ \tan A \cdot \tan B} @$

Untuk menambah pemahaman kita terkait Rumus Jumlah dan Selisih Dua Sudut Perbandingan Trigonometri ini, mari kita simak beberapa soal latihan di bawah ini.

Soal latihan dan pembahasan Rumus Jumlah dan Selisih Dua Sudut Perbandingan Trigonometri

1. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\sin 15^{\circ}=\cdots@$

@$\begin{align} (A)\ & \dfrac{1}{4} \left(\sqrt{2}-\sqrt{6} \right) \\ (B)\ & \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \\ (C)\ & \dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right) \\ (D)\ & \dfrac{1}{2} \left(\sqrt{2}+\sqrt{6} \right) \\ (E)\ & \dfrac{1}{2} \left(\sqrt{2}-\sqrt{6} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\sin 15^{\circ}@$ kita pilih dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\sin\left ( A-B \right ) & = \sin A \cdot \cos B- \sin B \cdot \cos A \\ \hline \sin 15^{\circ} & = \sin\left ( 45^{\circ}-30^{\circ} \right ) \\ & = \sin 45^{\circ} \cdot \cos 30^{\circ} - \sin 30^{\circ} \cdot \cos 45^{\circ} \\ & = \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2}\sqrt{3} - \dfrac{1}{2} \cdot \dfrac{1}{2}\sqrt{2} \\ & = \dfrac{1}{4}\sqrt{6} - \dfrac{1}{4}\sqrt{2} \\ & = \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(B)\ \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right)@$

2. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\cos 75^{\circ}=\cdots@$

@$\begin{align} (A)\ & \dfrac{1}{4} \left(\sqrt{2}-\sqrt{6} \right) \\ (B)\ & \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \\ (C)\ & \dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right) \\ (D)\ & \dfrac{1}{2} \left(\sqrt{2}+\sqrt{6} \right) \\ (E)\ & \dfrac{1}{2} \left(\sqrt{2}-\sqrt{6} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\cos 75^{\circ}@$ kita pilih dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\cos\left ( A+B \right ) & = \cos A \cdot \cos B - \sin A \cdot \sin A \\ \hline \cos 75^{\circ} & = \cos\left ( 45^{\circ}+30^{\circ} \right ) \\ & = \cos 45^{\circ} \cdot \cos 30^{\circ} - \sin 45^{\circ} \cdot \sin 30^{\circ} \\ & = \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2}\sqrt{3} - \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2} \\ & = \dfrac{1}{4}\sqrt{6} - \dfrac{1}{4}\sqrt{2} \\ & = \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \end{align}@$

Jika sudah mengetahui @$\sin 15^{\circ}=\dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right)@$ dapat juga kita gunakan sudut berelasi,
@$\begin{align}
\cos 75^{\circ} & = \cos \left( 90^{\circ} - 15^{\circ} \right) \\ \cos 75^{\circ} & = \sin 15^{\circ} \\ \cos 75^{\circ} & = \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(B)\ \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right)@$

3. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\sin 285^{\circ}=\cdots@$

@$\begin{align} (A)\ & \dfrac{1}{4} \left(\sqrt{2}-\sqrt{6} \right) \\ (B)\ & \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \\ (C)\ & \dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right) \\ (D)\ & -\dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right) \\ (E)\ & \dfrac{1}{2} \left(\sqrt{2}-\sqrt{6} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\sin 285^{\circ}@$ kita gunakan sudut berelasi dan dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\sin 285^{\circ} & = \sin \left ( 270^{\circ}+15^{\circ} \right ) \\ & = - \cos 15^{\circ} \\ \hline \cos\left ( A-B \right ) & = \cos A \cdot \cos B + \sin A \cdot \sin A \\ \hline \cos 15^{\circ} & = \cos\left ( 45^{\circ}-30^{\circ} \right ) \\ & = \cos 45^{\circ} \cdot \cos 30^{\circ} + \sin 45^{\circ} \cdot \sin 30^{\circ} \\ & = \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2} \\ & = \dfrac{1}{4}\sqrt{6} + \dfrac{1}{4}\sqrt{2} \\ & = \dfrac{1}{4} \left(\sqrt{6} + \sqrt{2} \right) \\ \hline \sin 285^{\circ} & = - \cos 15^{\circ} \\ & = - \dfrac{1}{4} \left(\sqrt{6} + \sqrt{2} \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(D)\ -\dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right)@$

4. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\cos 345^{\circ}=\cdots@$

@$\begin{align} (A)\ & \dfrac{1}{4} \left(\sqrt{2}-\sqrt{6} \right) \\ (B)\ & \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \\ (C)\ & \dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right) \\ (D)\ & \dfrac{1}{4} \left(\sqrt{2}+\sqrt{6} \right) \\ (E)\ & \dfrac{1}{2} \left(\sqrt{2}-\sqrt{6} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\cos 345^{\circ}@$ kita gunakan sudut berelasi dan dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\cos 345^{\circ} & = \cos \left ( 360^{\circ}-15^{\circ} \right ) \\ & = \cos 15^{\circ} \\ \hline \cos\left ( A-B \right ) & = \cos A \cdot \cos B + \sin A \cdot \sin A \\ \hline \cos 15^{\circ} & = \cos\left ( 45^{\circ}-30^{\circ} \right ) \\ & = \cos 45^{\circ} \cdot \cos 30^{\circ} + \sin 45^{\circ} \cdot \sin 30^{\circ} \\ & = \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2} \\ & = \dfrac{1}{4}\sqrt{6} + \dfrac{1}{4}\sqrt{2} \\ & = \dfrac{1}{4} \left(\sqrt{6} + \sqrt{2} \right) \\ \hline \cos 345^{\circ} & = \cos 15^{\circ} \\ & = \dfrac{1}{4} \left(\sqrt{6} + \sqrt{2} \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ \dfrac{1}{4} \left(\sqrt{6}+\sqrt{2} \right)@$

5. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\csc 195^{\circ}=\cdots@$

@$\begin{align} (A)\ & \left(\sqrt{6}-\sqrt{2} \right) \\ (B)\ & \left(\sqrt{6}+\sqrt{2} \right) \\ (C)\ & \left(\sqrt{2}-\sqrt{6} \right) \\ (D)\ & - \left(\sqrt{6}+\sqrt{2} \right) \\ (E)\ & \dfrac{1}{2} \left(\sqrt{6}-\sqrt{2} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\csc 195^{\circ}@$ kita gunakan sudut berelasi dan dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\csc 195^{\circ} & = \dfrac{1}{\sin 195^{\circ}} \\ & = \dfrac{1}{\sin \left ( 180^{\circ}+15^{\circ} \right )} \\ & = \dfrac{1}{- \sin 15^{\circ}} \\ \hline \sin \left ( A-B \right ) & = \sin A \cdot \cos B + \sin B \cdot \cos A \\ \hline \sin 15^{\circ} & = \sin\left ( 45^{\circ}-30^{\circ} \right ) \\ & = \sin 45^{\circ} \cdot \cos 30^{\circ} - \sin 30^{\circ} \cdot \cos 45^{\circ} \\ & = \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2}\sqrt{3} - \dfrac{1}{2} \cdot \dfrac{1}{2}\sqrt{2} \\ & = \dfrac{1}{4}\sqrt{6} - \dfrac{1}{4}\sqrt{2} \\ & = \dfrac{1}{4} \left(\sqrt{6}-\sqrt{2} \right) \\ \csc 195^{\circ} & = -\dfrac{1}{\sin 15^{\circ}} \\ & = -\dfrac{1}{\frac{1}{4} \left(\sqrt{6} - \sqrt{2} \right)} \times \dfrac{\sqrt{6} + \sqrt{2}}{\sqrt{6} + \sqrt{2}} \\ & = -\dfrac{\sqrt{6} + \sqrt{2}}{\frac{1}{4} \left( 6 - 2 \right)} \\ & = - \left( \sqrt{6} + \sqrt{2} \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(D)\ - \left(\sqrt{6}+\sqrt{2} \right)@$

6. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\sec 345^{\circ}=\cdots@$

@$\begin{align} (A)\ & \left(\sqrt{6}-\sqrt{2} \right) \\ (B)\ & \left(\sqrt{6}+\sqrt{2} \right) \\ (C)\ & \left(\sqrt{2}-\sqrt{6} \right) \\ (D)\ & - \left(\sqrt{6}+\sqrt{2} \right) \\ (E)\ & \dfrac{1}{2} \left(\sqrt{6}-\sqrt{2} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\csc 195^{\circ}@$ kita gunakan sudut berelasi dan dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\sec 345^{\circ} & = \dfrac{1}{\cos 345^{\circ}} \\ & = \dfrac{1}{\cos \left ( 360^{\circ}-15^{\circ} \right )} \\ & = \dfrac{1}{\cos 15^{\circ}} \\ \hline \cos\left ( A-B \right ) & = \cos A \cdot \cos B + \sin A \cdot \sin A \\ \hline \cos 15^{\circ} & = \cos\left ( 45^{\circ}-30^{\circ} \right ) \\ & = \cos 45^{\circ} \cdot \cos 30^{\circ} + \sin 45^{\circ} \cdot \sin 30^{\circ} \\ & = \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2}\sqrt{3} + \dfrac{1}{2}\sqrt{2} \cdot \dfrac{1}{2} \\ & = \dfrac{1}{4}\sqrt{6} + \dfrac{1}{4}\sqrt{2} \\ & = \dfrac{1}{4} \left(\sqrt{6} + \sqrt{2} \right) \\ \hline \sec 345^{\circ} & = \dfrac{1}{\cos 15^{\circ}} \\ & = \dfrac{1}{\frac{1}{4} \left(\sqrt{6} + \sqrt{2} \right)} \times \dfrac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}} \\ & = \dfrac{\sqrt{6} - \sqrt{2}}{\frac{1}{4} \left( 6 - 2 \right)} \\ & = \sqrt{6} - \sqrt{2} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(A)\ \left(\sqrt{6}-\sqrt{2} \right)@$

7. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\tan 195^{\circ}=\cdots@$

@$\begin{align} (A)\ & 2+\sqrt{3} \\ (B)\ & 2-\sqrt{3} \\ (C)\ & \sqrt{3} - 2 \\ (D)\ & - \left(2+\sqrt{3} \right) \\ (E)\ & \dfrac{1}{2} \left(2+ \sqrt{3} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\tan 195^{\circ}@$ kita gunakan sudut berelasi dan dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\tan 195^{\circ} & = \tan \left ( 180^{\circ}+15^{\circ} \right ) \\ & = \tan 15^{\circ} \\ \hline \tan \left ( A-B \right ) & = \dfrac{ \tan A - \tan B}{1 + \tan A \cdot \tan B} \\ \hline \tan 15^{\circ} & = \tan \left( 45^{\circ} - 30^{\circ} \right) \\ & = \dfrac{ \tan 45^{\circ} - \tan 30^{\circ}}{1 + \tan 45^{\circ} \cdot \tan 30^{\circ}} \\ & = \dfrac{ 1 - \frac{1}{3}\sqrt{3} }{1 + 1 \cdot \frac{1}{3}\sqrt{3}} \\ & = \dfrac{ \frac{3}{3} - \frac{\sqrt{3}}{3} }{\frac{3}{3} + \frac{\sqrt{3}}{3}} \\ & = \dfrac{ 3 - \sqrt{3} }{ 3 + \sqrt{3} } \times \dfrac{ 3 - \sqrt{3} }{ 3 - \sqrt{3} } \\ & = \dfrac{ 9 - 6 \sqrt{3} + 3 }{ 9 - 3 } \\ & = \dfrac{ 12 - 6 \sqrt{3} }{ 6 } \\ & = 2 - \sqrt{3} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(B)\ 2-\sqrt{3}@$

8. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\cot 345^{\circ}=\cdots@$

@$\begin{align} (A)\ & 2+\sqrt{3} \\ (B)\ & 2-\sqrt{3} \\ (C)\ & \sqrt{3} - 2 \\ (D)\ & - \left(2+\sqrt{3} \right) \\ (E)\ & \dfrac{1}{2} \left(2+ \sqrt{3} \right) \end{align}@$

Pembahasan:

Untuk menghitung nilai @$\cot 345^{\circ}@$ kita gunakan sudut berelasi dan dari keenam rumus jumlah dan selisih dua sudut perbandingan trigonometri kita pilih yang paling cocok digunakan:
@$\begin{align}
\cot 345^{\circ} & = \dfrac{1}{\tan 345^{\circ}} \\ & = \dfrac{1}{\tan \left ( 360^{\circ}-15^{\circ} \right )} \\ & = \dfrac{1}{-\tan 15^{\circ}} \\ \hline \tan \left ( A-B \right ) & = \dfrac{ \tan A - \tan B}{1 + \tan A \cdot \tan B} \\ \hline \tan 15^{\circ} & = \tan \left ( 45^{\circ} - 30^{\circ} \right ) \\ & = \dfrac{ \tan 45^{\circ} - \tan 30^{\circ}}{1 + \tan 45^{\circ} \cdot \tan 30^{\circ}} \\ & = \dfrac{ 1 - \frac{1}{3}\sqrt{3} }{1 + 1 \cdot \frac{1}{3}\sqrt{3}} \\ & = \dfrac{ \frac{3}{3} - \frac{\sqrt{3}}{3} }{\frac{3}{3} + \frac{\sqrt{3}}{3}} \\ & = \dfrac{ 3 - \sqrt{3} }{ 3 + \sqrt{3} } \times \dfrac{ 3 - \sqrt{3} }{ 3 - \sqrt{3} } \\ & = \dfrac{ 9 - 6 \sqrt{3} + 3 }{ 9 - 3 } \\ & = \dfrac{ 12 - 6 \sqrt{3} }{ 6 } \\ & = 2 - \sqrt{3} \\ \cot 345^{\circ} & = \dfrac{1}{-\tan 15^{\circ}} \\ & = \dfrac{1}{- \left( 2 - \sqrt{3} \right)} \times \dfrac{2+\sqrt{3}}{2+\sqrt{3}} \\ & = \dfrac{2+\sqrt{3}}{- \left( 4-3 \right)} \\ & = - \left( 2+\sqrt{3} \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(D)\ - \left(2+\sqrt{3} \right)@$

9. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Diketahui @$\sin \alpha = \dfrac{3}{5}@$ dan @$\cos \beta = \dfrac{12}{13}@$ dengan @$\alpha@$ sudut tumpul dan @$\beta@$ sudut lancip. Nilai dari @$\sin \left( \alpha + \beta \right)=\cdots@$

@$\begin{align} (A)\ & \dfrac{16}{63} \\ (B)\ & -\dfrac{16}{63} \\ (C)\ & \dfrac{16}{65} \\ (D)\ & -\dfrac{16}{63} \\ (E)\ & \dfrac{56}{65} \end{align}@$

Pembahasan:

Dari @$\sin \alpha = \dfrac{3}{5}@$ dan @$\cos \beta = \dfrac{12}{13}@$ dengan @$\alpha@$ sudut tumpul dan @$\beta@$ sudut lancip dapat kita peroleh:

Dari apa yang kita peroleh di atas dapat kita hitung:
@$\begin{align}
\sin \left( \alpha + \beta \right) & = \sin \alpha \cdot \cos \beta + \sin \beta \cdot \cos \alpha \\ & = \dfrac{3}{5} \cdot \dfrac{12}{13} + \dfrac{5}{13} \cdot \left(- \dfrac{4}{5} \right) \\ & = \dfrac{36}{65} - \dfrac{20}{65} \\ & = \dfrac{16}{65} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ \dfrac{16}{65}@$

10. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Diketahui @$\sin \alpha = -\dfrac{12}{13}@$ dan @$\cos \beta = -\dfrac{4}{5}@$ dengan @$\alpha@$ dikuadran ke III dan @$\beta@$ dikuadran ke II. Nilai dari @$\cos \left( \alpha - \beta \right)=\cdots@$

@$\begin{align} (A)\ & \dfrac{56}{65} \\ (B)\ & -\dfrac{56}{65} \\ (C)\ & \dfrac{16}{65} \\ (D)\ & -\dfrac{16}{65} \\ (E)\ & \dfrac{12}{65} \end{align}@$

Pembahasan:

Dari @$\sin \alpha = -\dfrac{12}{13}@$ dan @$\cos \beta = -\dfrac{4}{5}@$ dengan @$\alpha@$ dikuadran ke III dan @$\beta@$ dikuadran ke II dapat kita peroleh:

Dari apa yang kita peroleh di atas dapat kita hitung:
@$\begin{align}
\cos \left( \alpha - \beta \right) & = \cos \alpha \cdot \cos \beta + \sin \alpha \cdot \sin \beta \\ & = \left(- \dfrac{5}{13} \right) \cdot \left( -\dfrac{4}{5} \right) + \left(- \dfrac{12}{13} \right) \cdot \left( \dfrac{3}{5} \right) \\ & = \dfrac{20}{65} - \dfrac{36}{65} \\ & = -\dfrac{16}{65} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(D)\ -\dfrac{16}{65}@$

11. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Diketahui @$\sin \alpha = \dfrac{5}{13}@$ dan @$\sin \beta = -\dfrac{4}{5}@$ dimana @$90^{\circ} \lt \alpha \lt 180^{\circ}@$ dan @$270^{\circ} \lt \beta \lt 360^{\circ}@$. Nilai dari @$\tan \left( \alpha + \beta \right)=\cdots@$

@$\begin{align} (A)\ & \dfrac{42}{16} \\ (B)\ & \dfrac{63}{16} \\ (C)\ & -\dfrac{63}{16} \\ (D)\ & \dfrac{33}{56} \\ (E)\ & -\dfrac{21}{8} \end{align}@$

Pembahasan:

Dari @$\sin \alpha = \dfrac{5}{13}@$ dan @$\sin \beta = -\dfrac{4}{5}@$ dimana @$90^{\circ} \lt \alpha \lt 180^{\circ}@$ dan @$270^{\circ} \lt \beta \lt 360^{\circ}@$ dapat kita peroleh:

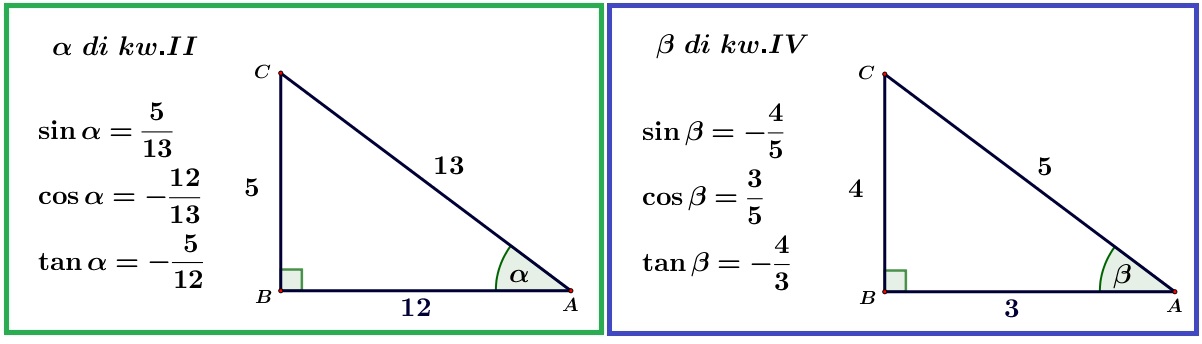
Dari apa yang kita peroleh di atas dapat kita hitung:
@$\begin{align}
\tan \left( \alpha + \beta \right) & = \dfrac{ \tan \alpha + \tan \beta}{1- \tan \alpha \cdot \tan \beta} \\ & = \dfrac{ \left(- \frac{5}{12} \right) +\left(- \frac{4}{3} \right)}{1- \left(- \frac{5}{12} \right) \cdot \left(- \frac{4}{3} \right)} \\ & = \dfrac{ \frac{-15-48}{36}}{1- \frac{20}{36} } \\ & = \dfrac{ -\frac{63}{36}}{ \frac{16}{36} } \\ & = -\dfrac{63}{16} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ -\dfrac{63}{16}@$

12. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai @$\dfrac{\tan \alpha + \tan \beta}{\tan \alpha - \tan \beta}@$ setara dengan...

@$\begin{align} (A)\ & \dfrac{\sin \left( \alpha + \beta \right)}{\cos \left( \alpha - \beta \right)} \\ (B)\ & \dfrac{\sin \left( \alpha - \beta \right)}{\cos \left( \alpha + \beta \right)} \\ (C)\ & \dfrac{\sin \left( \alpha + \beta \right)}{\sin \left( \alpha - \beta \right)} \\ (D)\ & \dfrac{\cos \left( \alpha + \beta \right)}{\cos \left( \alpha - \beta \right)} \\ (E)\ & \dfrac{\sin \left( \alpha - \beta \right)}{\sin \left( \alpha - \beta \right)} \end{align}@$

Pembahasan:

Dengan menggunakan @$\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}@$ kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
\dfrac{\tan \alpha + \tan \beta}{\tan \alpha - \tan \beta} & = \dfrac{\frac{\sin \alpha}{\cos \alpha} + \frac{\sin \beta}{\cos \beta}}{\frac{\sin \alpha}{\cos \alpha} - \frac{\sin \beta}{\cos \beta}} \\ & = \dfrac{\frac{\sin \alpha \cdot \cos \beta + \sin \beta \cdot \cos \alpha}{\cos \alpha \cdot \cos \beta}}{\frac{\sin \alpha \cdot \cos \beta - \sin \beta \cdot \cos \alpha}{\cos \alpha \cdot \cos \beta}} \\ & = \dfrac{ \sin \alpha \cdot \cos \beta + \sin \beta \cdot \cos \alpha}{ \sin \alpha \cdot \cos \beta - \sin \beta \cdot \cos \alpha} \\ & = \dfrac{ \sin \left( \alpha + \beta \right)}{ \sin \left( \alpha - \beta \right)} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ \dfrac{\sin \left( \alpha + \beta \right)}{\sin \left( \alpha - \beta \right)}@$

13. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai dari @$\dfrac{\cos \left( \alpha + \beta \right)}{\cos \alpha \cdot \cos \beta}@$ setara dengan...

@$\begin{align} (A)\ & 1 + \sin \alpha \cdot \cos \beta \\ (B)\ & 1 - \sin \alpha \cdot \sin \beta \\ (C)\ & 1 + \tan \alpha \cdot \tan \beta \\ (D)\ & 1 - \tan \alpha \cdot \tan \beta \\ (E)\ & 1 + \cos \alpha \cdot \cos \beta \end{align}@$

Pembahasan:

Dengan menggunakan @$ \cos \left ( \alpha + \beta \right )=\cos \alpha \cdot \cos \beta -\sin \alpha \cdot \sin \beta @$ kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
\dfrac{\cos \left( \alpha + \beta \right)}{\cos \alpha \cdot \cos \beta} & = \dfrac{\cos \alpha \cdot \cos \beta -\sin \alpha \cdot \sin \beta}{\cos \alpha \cdot \cos \beta} \\ & = \dfrac{\cos \alpha \cdot \cos \beta}{\cos \alpha \cdot \cos \beta} - \dfrac{\sin \alpha \cdot \sin \beta}{\cos \alpha \cdot \cos \beta}\\ & = 1 - \tan \alpha \cdot \tan \beta \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(D)\ 1 - \tan \alpha \cdot \tan \beta@$

14. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

@$\sin \alpha + \sin \left( \alpha + 120^{\circ} \right) + \cos \left( 210^{\circ} - \alpha \right)=\cdots@$

@$\begin{align} (A)\ & 0 \\ (B)\ & 1 \\ (C)\ & 2 \\ (D)\ & 3 \\ (E)\ & 4 \end{align}@$

Pembahasan:

Untuk menyederhanakan @$\sin \alpha + \sin \left( \alpha + 120^{\circ} \right) + \cos \left( 210^{\circ} - \alpha \right)@$ kita coba kerjakan beberapa bagian secara terpisah seperti berikut ini:

@$\begin{align}
\sin \left( \alpha + 120^{\circ} \right) & = \sin \alpha \cdot \cos 120^{\circ} + \sin 120^{\circ} \cdot \cos \alpha \\ & = \sin \alpha \cdot \cos \left( 90^{\circ} + 30^{\circ} \right) - \sin \left( 90^{\circ} + 30^{\circ} \right) \cdot \cos \alpha \\ & = - \sin \alpha \cdot \sin 30^{\circ} + \cos 30^{\circ} \cdot \cos \alpha \\ & = -\dfrac{1}{2} \sin \alpha + \dfrac{1}{2}\sqrt{3} \cos \alpha \\ \hline \cos \left( 210^{\circ} - \alpha \right) & = \cos 210^{\circ} \cdot \cos \alpha + \sin 210^{\circ} \cdot \sin \alpha \\ & = \cos \left( 180^{\circ} + 30^{\circ} \right) \cdot \cos \alpha + \sin \left( 180^{\circ} + 30^{\circ} \right) \cdot \sin \alpha \\ & = -\dfrac{1}{2}\sqrt{3} \cos \alpha - \dfrac{1}{2} \sin \alpha \\ \end{align}@$

Dari hasil di atas kita peroleh:
@$\begin{align}
& \sin \alpha + \sin \left( \alpha + 120^{\circ} \right) + \cos \left( 210^{\circ} - \alpha \right) \\ & = \sin \alpha -\dfrac{1}{2} \sin \alpha + \dfrac{1}{2}\sqrt{3} \cos \alpha + -\dfrac{1}{2}\sqrt{3} \cos \alpha - \dfrac{1}{2} \sin \alpha \\ & = \sin \alpha - \sin \alpha \\ & = 0 \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(A)\ 0@$

15. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Nilai @$\tan \left( 45^{\circ} + \alpha \right)@$ setara dengan...

@$\begin{align} (A)\ & \dfrac{\cos \alpha - \sin \alpha}{\cos \alpha + \sin \alpha} \\ (B)\ & \dfrac{\cos \alpha + \sin \alpha}{\cos \alpha - \sin \alpha} \\ (C)\ & \dfrac{\sin \alpha - \cos \alpha}{\sin \alpha + \cos \alpha} \\ (D)\ & \dfrac{\sin \alpha + \cos \alpha}{\sin \alpha - \cos \alpha} \\ (E)\ & \dfrac{\sin \alpha}{\sin \alpha + \cos \alpha} \end{align}@$

Pembahasan:

Dengan menggunakan @$ \tan \left ( A+B \right )=\dfrac{ \tan A+ \tan B}{1- \tan A\cdot \tan B} @$ dan manipulasi aljabar kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
\tan \left( 45^{\circ} + \alpha \right) & = \dfrac{ \tan 45^{\circ}+ \tan \alpha}{1- \tan 45^{\circ} \cdot \tan \alpha} \\ & = \dfrac{ 1 + \tan \alpha}{1- 1 \cdot \tan \alpha} \\ & = \dfrac{ 1 + \frac{\sin \alpha}{\cos \alpha}}{1- \frac{\sin \alpha}{\cos \alpha}} \\ & = \dfrac{ \frac{\cos \alpha}{\cos \alpha} + \frac{\sin \alpha}{\cos \alpha}}{\frac{\cos \alpha}{\cos \alpha}- \frac{\sin \alpha}{\cos \alpha}} \\ & = \dfrac{ \frac{\cos \alpha+\sin \alpha}{\cos \alpha}}{\frac{\cos \alpha-\sin \alpha}{\cos \alpha}} \\ & = \dfrac{ \cos \alpha+\sin \alpha }{ \cos \alpha-\sin \alpha } \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(B)\ \dfrac{ \cos \alpha+\sin \alpha }{ \cos \alpha-\sin \alpha }@$

16. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Jika @$3 \cdot \cos \left( \alpha+\beta \right)=\cos \left( \alpha - \beta \right)@$ maka nilai @$\tan \alpha \cdot \tan \beta =\cdots@$

@$\begin{align} (A)\ & -\dfrac{3}{2} \\ (B)\ & \dfrac{3}{2} \\ (C)\ & \dfrac{1}{2} \\ (D)\ & -\dfrac{1}{2} \\ (E)\ & 2 \end{align}@$

Pembahasan:

Dengan menggunakan rumus jumlah dan selisih dua sudut pada cosinus dan manipulasi aljabar kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
3 \cdot \cos \left( \alpha+\beta \right) & = \cos \left( \alpha - \beta \right) \\ 3 \cdot \left( \cos \alpha \cdot \cos \beta-\sin \alpha \cdot \sin \beta \right) & = \cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta \\ 3\cos \alpha \cdot \cos \beta-3\sin \alpha \cdot \sin \beta & = \cos \alpha \cdot \cos \beta+\sin \alpha \cdot \sin \beta \\ 2\cos \alpha \cdot \cos \beta & =4\sin \alpha \cdot \sin \beta \\ \dfrac{2}{4} & =\dfrac{\sin \alpha \cdot \sin \beta}{\cos \alpha \cdot \cos \beta} \\ \dfrac{1}{2} & =\tan \alpha \cdot \tan \beta \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ \dfrac{1}{2}@$

17. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

Jika @$m=\sin A + \sin B@$ dan @$n=\cos A + \cos B@$ maka nilai @$m^{n}+n^{2} =\cdots@$

@$\begin{align} (A)\ & 2+2 \cdot \sin \left( A-B \right) \\ (B)\ & 2-2 \cdot \sin \left( A-B \right) \\ (C)\ & 2+2 \cdot \cos \left( A-B \right) \\ (D)\ & 2-2 \cdot \cos \left( A-B \right) \\ (E)\ & 2-2 \cdot \cos \left( A+B \right) \end{align}@$

Pembahasan:

Dengan menggunakan rumus jumlah dan selisih dua sudut pada cosinus dan manipulasi aljabar kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
m^{n}+n^{2} & = \left( \sin A + \sin B \right)^{2}+\left( \cos A + \cos B \right)^{2} \\ & = \sin^{2} A + \sin^{2} B+2 \sin A\ \sin B+ \cos^{2} A + \cos B^{2}+ 2 \cos A\ \cos B \\ & = \sin^{2} A + \cos^{2} A + \sin^{2} B + \cos B^{2}+2 \sin A\ \sin B + 2 \cos A\ \cos B \\ & = 1 + 1 + 2 \left( \sin A\ \sin B+ \cos A\ \cos B \right) \\ & = 2 + 2 \cdot \cos \left( A-B \right) \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ 2+2 \cdot \cos \left( A-B \right)@$

18. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

@$\sin 165^{\circ} \cdot \cos 15^{\circ} + \cos 165^{\circ} \cdot \sin 15^{\circ} =\cdots@$

@$\begin{align} (A)\ & -\dfrac{1}{2}\sqrt{3} \\ (B)\ & -\dfrac{1}{2} \\ (C)\ & 0 \\ (D)\ & \dfrac{1}{2} \\ (E)\ & \dfrac{1}{2}\sqrt{3} \end{align}@$

Pembahasan:

Dengan menggunakan rumus @$ \sin \left ( A+B \right )=\sin A \cdot \cos B+\sin B \cdot \cos A @$ dan manipulasi aljabar kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
\sin \left ( A+B \right ) & = \sin A \cdot \cos B+\sin B \cdot cosA \\ \hline & \sin 165^{\circ} \cdot \cos 15^{\circ} + \cos 165^{\circ} \cdot \sin 15^{\circ} \\ & = \sin \left( 165^{\circ}+ 15^{\circ} \right) \\ & = \sin 180^{\circ} \\ & = 0 \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(C)\ 0@$

19. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

@$4 \cdot \cos 200^{\circ} \cdot \cos 10^{\circ} - 4 \sin 200^{\circ} \cdot \sin 10^{\circ} =\cdots@$

@$\begin{align} (A)\ & 2\sqrt{3} \\ (B)\ & -2\sqrt{3} \\ (C)\ & \sqrt{3} \\ (D)\ & -\sqrt{3} \\ (E)\ & \dfrac{1}{2}\sqrt{3} \end{align}@$

Pembahasan:

Dengan menggunakan rumus @$ \cos \left ( A+B \right )=\cos A \cdot \cos B-\sin A \cdot \sin B @$ dan manipulasi aljabar kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
\cos \left ( A+B \right )&\cos A \cdot \cos B-\sin A \cdot \sin B \\ \hline & 4 \cdot \cos 200^{\circ} \cdot \cos 10^{\circ} - 4 \sin 200^{\circ} \cdot \sin 10^{\circ} \\ & = 4 \left( \cos 200^{\circ} \cdot \cos 10^{\circ} - \sin 200^{\circ} \cdot \sin 10^{\circ} \right) \\ & = 4 \left( \cos \left( 200^{\circ}+ 10^{\circ} \right) \right) \\ & = 4 \cdot \cos 210^{\circ} \\ & = 4 \cdot \cos \left(180^{\circ} + 30^{\circ} \right) \\ & = 4 \cdot \left(-\cos 30^{\circ} \right) \\ & = 4 \cdot \left(- \dfrac{1}{2}\sqrt{3} \right) \\ & = -2\sqrt{3} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(B)\ -2\sqrt{3}@$

20. Soal Latihan Rumus Jumlah dan Selisih Dua Sudut

@$\cos 80^{\circ} \cdot \sin 20^{\circ} - \sin 80^{\circ} \cdot \cos 20^{\circ} =\cdots@$

@$\begin{align} (A)\ & \dfrac{1}{2} \\ (B)\ & -\dfrac{1}{2} \\ (C)\ & \dfrac{1}{2}\sqrt{2} \\ (D)\ & -\dfrac{1}{2}\sqrt{2} \\ (E)\ & -\dfrac{1}{2}\sqrt{3} \end{align}@$

Pembahasan:

Dengan menggunakan rumus @$ \sin \left ( A-B \right )=\sin A \cdot \cos B-\sin B \cdot \cos A @$ dan manipulasi aljabar kita coba sederhanakan bentuk di atas menjadi seperti berikut ini:

@$\begin{align}
\sin \left ( A - B \right ) & = \sin A \cdot \cos B - \sin B \cdot cosA \\ \hline & \cos 80^{\circ} \cdot \sin 20^{\circ} - \sin 80^{\circ} \cdot \cos 20^{\circ} \\ & = \sin 20^{\circ} \cdot \cos 80^{\circ} - \sin 80^{\circ} \cdot \cos 20^{\circ} \\ & = \sin \left( 20^{\circ} - 80^{\circ} \right) \\ & = \sin \left( - 60^{\circ} \right) \\ & = - \sin 60^{\circ} \\ & = -\dfrac{1}{2}\sqrt{3} \end{align}@$

@$\therefore@$ Pilihan yang sesuai adalah @$(E)\ -\dfrac{1}{2}\sqrt{3}@$